Tail Recursion - An Optimization Technique

September 9, 2025

I’m pretty sure you’ve already heard about recursion. If not, check out these videos first:

Now, let’s move on to tail recursion, and why it matters for embedded systems.

What is Tail Recursion?
Normal Recursion Example (Factorial)
Tail Recursion Example
Tail Recursion in Embedded Systems
Conclusion
References

What is Tail Recursion?

A function is tail-recursive when the recursive call is the last thing it does—no extra work is left afterwards. This means the function doesn’t need to “remember” the previous state. As a result, tail recursion uses less memory, and compilers like GCC or Clang can optimize it further.

If it’s not clear now, just wait a little longer..trust me!

Normal Recursion Example (Factorial)

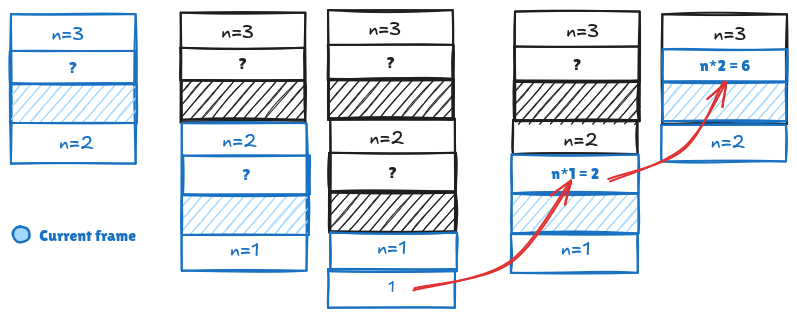
Let’s look at the factorial of 3 using normal recursion:

factorial(3)
→ 3 * factorial(2)
→ 3 * (2 * factorial(1))
→ 3 * (2 * (1 * factorial(0)))
→ 3 * (2 * (1 * 1))   # factorial(0) = 1
→ 3 * (2 * 1)
→ 3 * 2
→ 6

During recursion, values pile up in the stack (return addresses, arguments, partial results). This uses a lot of memory before the calculation even starts to unwind.

normal recursion stack

Tail Recursion Example

Now, the same factorial but with tail recursion. In this case, we use an extra parameter - an accumulator (acc):

factorial_tail(3, 1)        // acc = 1
→ factorial_tail(2, 3)      // acc = 3
→ factorial_tail(1, 6)      // acc = 6
→ factorial_tail(0, 6)  = 6

Here the accumulator carries the result along, so there’s no need to keep track of all previous calls.

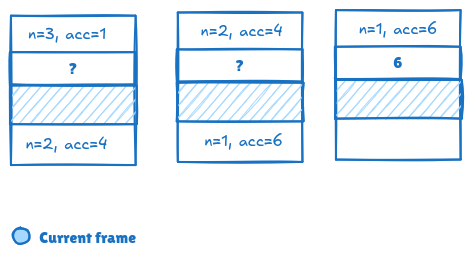
tail recursion stack

This makes tail recursion more memory-efficient, because the compiler only needs to store the current state (n and acc).

Note: GCC and Clang can optimize tail-recursive functions to avoid growing the call stack, effectively turning them into loops. This means if you use -O2 or -O3 optimization flags or -foptimize-sibling-calls, you could write recursive functions without worrying about stack overflow for deep recursions.

Tail Recursion in Embedded Systems

Why should you care? Well… In embedded systems you often have very limited memory and processing power.

One practical use case is in data filtering, like a Kalman filter for sensor streams. Here’s a simplified C code for kalman filtering using tail recursion:

// Tail-recursive Kalman filter update
KalmanState kalman_update_recursive(KalmanState state, 
                                    const float* measurements, 
                                    int index, int count, 
                                    float process_noise, 
                                    float measurement_noise) {
    if (index >= count) return state; // Base case

    float m = measurements[index];
    float predicted_cov = state.error_covariance + process_noise;
    float gain = predicted_cov / (predicted_cov + measurement_noise);

    KalmanState new_state = {
        .estimate = state.estimate + gain * (m - state.estimate),
        .error_covariance = (1 - gain) * predicted_cov
    };

    return kalman_update_recursive(new_state, measurements, index + 1, count, process_noise, measurement_noise);
}

Conclusion

Tail recursion is a powerful technique that can help optimize memory. Even though it’s often used in mathematical computation or signal processing, it’s still relevant in embedded systems where resources are limited and we deal with data streams.